一変量解析
一変量解析とは
例)賢い囚人スタット
ある刑務所では毎朝1個のパンが支給されます。囚人のスタットは自分に配られるパンの大きさが毎朝かなりばらついているのが気になっていました。
- 「今日は少し大きめだ」
- 「今日はかなり小さい」
- 「同じ大きさに作るのは難しいから仕方がないかな」
などと思っていました。
しかし、パンが小さい日の方が多いような気がしたため、それから毎日大きさを測ることにしました。

数日後、スタットはパンを配る看守の不正に気が付きました。その看守はリベートを払っている囚人に対して、意識的に大きいパンを配っていたのです。 スタットは大きさを測った結果を刑務所の所長に見せました。
看守は「時々スタットにも大きいパンを配り、ばれないようにしていたのだが…」と、不思議がっていたとのことです。
一変量解析で代表的な手法がヒストグラムです。
この「賢い囚人スタット」の例で、パンの大きさデータを適当な等間隔のクラスに分けてグラフにしたものが図1です。パン職人が同じ大きさになるように作れば、パンはこのような左右対象な分布(正規分布)になるでしょう。
※あくまでも、一定の目標値になるように製造し続けた場合に限り、コントロールできなかった誤差の影響で過大も過小も同程度に起きるため、左右対称に分布します。全ての社会現象が必ずしも正規分布に従うものではありません。
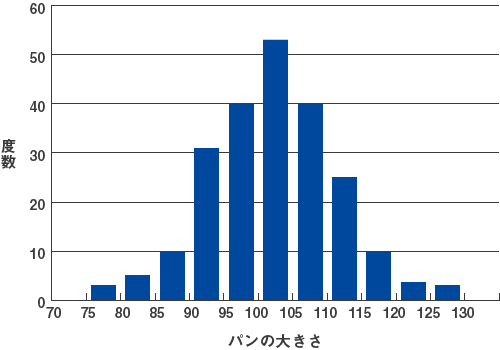
図1 正規分布(左右対称できれい)
ところが、"意識的に小さめのパンを配り、時々大きなパンを混ぜる"ということをすると、配られたパンは図2のような分布になってしまいます。配られたパンは、作られたパンの母集団を代表していないことになるのです。賢い囚人スタットは、このようにして看守の不正をあばいたのでした。
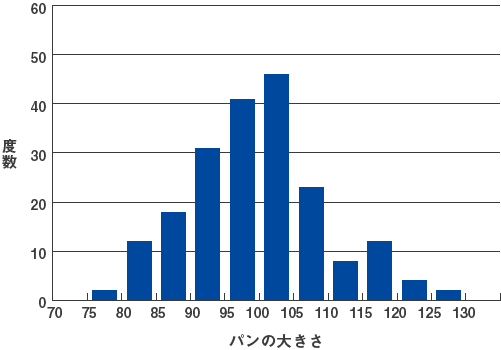
図2 偏りのある分布(右の方にもう1つのピークがある)
一変量解析をする上での指標に、平均値(すべての個別データを足し合わせた合計を、データの個数で割り算した値)、中央値(データを大きさの順に並べてちょうど真ん中にくる値)、最頻値(該当ケースが最も集中しているデータ値)、分散、標準偏差などがあります。それらのイメージを図で表したのが図3です。一変量解析はその他にも、箱ひげ図や、度数折れ線グラフ等があり、多変量解析を実施する前のデータクリーニングに使用されます。
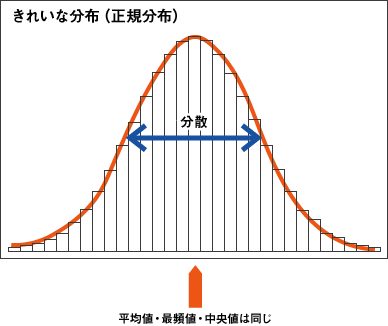
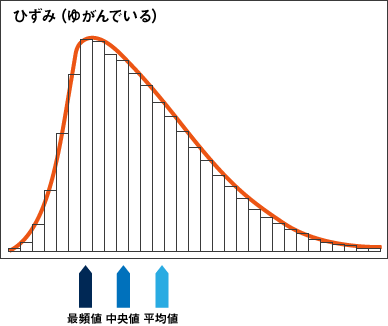
図3 分散、中央値、平均値、最頻値










