主成分分析
主成分分析とは、多変量データを統合し、新たな総合指標を作り出すための手法です。
主成分分析のモデルと、基本式
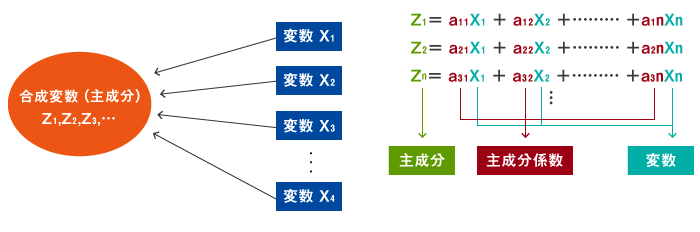
多くの変数に重み(ウェイト)をつけて少数の合成変数を作るのが主成分分析です。重みのつけ方は合成変数ができるだけ多く元の変数の情報量を含むようにします。できるだけ多くの情報をもつ合成変数(主成分)を順次作っていきます。
分析の手順
合成変数ができるだけ多くの情報量を持つようにするため、データの散らばり具合(分散)に着目します。これは、分散=情報量といえるからです。
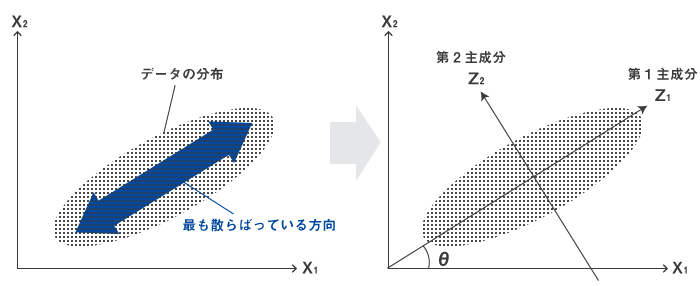
平面で示すためにデータが2次元(2変量)の場合で考えてみると、主成分スコアの分散が最も大きくなる方向に軸をとり、これを第1主成分とします。第1主成分だけでは元のデータが持っていた情報をすべて表すことは不可能です。そこで、次に分散が大きくなる方向に軸を取り、これを第2主成分とします。第2主成分の軸は第1主成分の軸に直交するように定めます。
分析結果の読み方
主成分分析で得られる指標
-
固有値
- 主成分分析を行うと、各主成分に対応した固有値が求まります。この固有値は主成分の分散に対応しており、その主成分がどの程度元のデータの情報を保持しているかを表します。
-
寄与率
- ある主成分の固有値が表す情報が、データのすべての情報の中でどの位の割合を占めるかを表します。変数全体の分散の合計に占める、その主成分のスコアの分散構成比を意味します。
-
累積寄与率
- 各主成分の寄与率を大きい順に足しあげていったもので、そこまでの主成分で、データの持っていた情報量がどのくらい説明されているかを示します。
主成分の数の選択
-
累積寄与率を基準とする
- 全体の情報の7、8割がカバーできていればよいという考え方から、累積寄与率が、70~80%に達するところまでの、主成分数を採用します。
主成分の意味の解釈
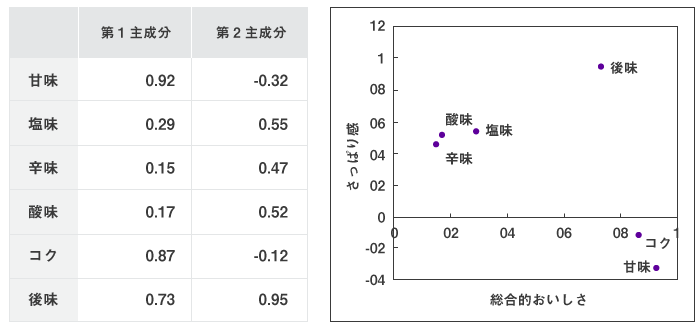
各主成分の主成分係数に着目して各主成分の意味を解釈します。第1主成分は総合指標になることが多く、下の例では、製品の総合的なおいしさを表していると言えるでしょう。また第2主成分はさっぱりしたおいしさを表していると解釈できます。この2つの主成分から項目をプロットすると下図のようになり、この2つの主成分に関しては、「コクと甘味」、「酸味と塩味と辛味」がそれぞれグループを作っていることが分かります。主成分は互いに直交するように定まっていますので、重複や同義の解釈をしないように気をつけましょう。
「重厚な第1主成分」「どっしりした第2主成分」などは悪い命名の一例です。