因子分析
因子分析とは
因子分析とは、多変量データに潜む共通因子を探り出すための手法として、消費者を理解するためによく使われる多変量解析手法です。
因子分析は「知能」という潜在的な概念を研究する中から生まれた分析手法です(Spearman, 1904)。これは目には見えず、直接測ることができない「知能」というものが存在し、それが具体的な知能テストや試験などの結果として現れる(観測できる)という考え方を元にしています。様々な事象(観測変数)を手がかりにして、潜在的に存在する概念(潜在変数)を推定するしかない、ということになります。
このような考え方の視点を広げてみると、消費者の意識、態度は全て潜在的な概念と考えることができ、具体的にモデルを描くと以下の図1のようになります。楕円が「悲しい気持ち」という潜在変数で、共通因子といいます。そして四角のX1~X3までの観測変数が、私達が見ることができる実際の現象と言うことができます。もちろん他の観測変数でも、「悲しい」という心が表出する可能性はあるでしょう。
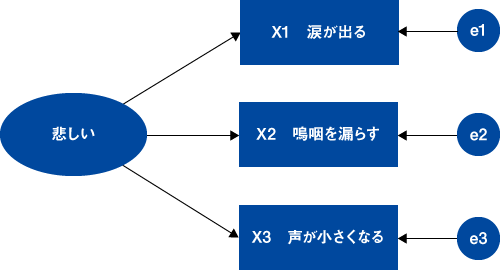
図1
また、この図にあるe1~e3は独自因子といい、それぞれの観測変数に固有の情報を表しています。つまり、それぞれの観測変数が以下のような形で分解されることになります。
観測変数 = 共通因子 + 独自因子
観測変数 = 共通因子 + 独自因子の統計的な概念を図示すると、図2のようになります。
観測変数zを共通因子空間S(F)で説明するとして、zのなかでS(F)で説明できる部分はhとなり、できなかった部分がeとなります。ここで、eとhは直行するので、z,h,eで直角三角形ができます。このことが、zをhとeに分解する、という意味になり、ピタゴラスの定理が分散分析の根拠になっています。
通常、分析をするにあたって関心を持つのは共通因子の方になりますので、単純に「因子」といったときは独自因子ではなく、共通因子を指します。ここで着目していただきたいのが、観測変数の全てを説明するモデルを作るのではなく、他の観測変数の中から共通する部分だけを共通因子空間によって説明し、それだけでは説明できない固有の要素を独自変数として残す、という点です。つまり、より小さな変数で人々の意識を理解する試みが行われており、「枝葉を捨てて、エッセンスを見る」というのが根本的な考え方となっています。この時、それぞれの観測変数に固有の枝が独自因子eと言うことができます。(朝野熙彦「マーケティング・リサーチ」講談社の第2章から引用)
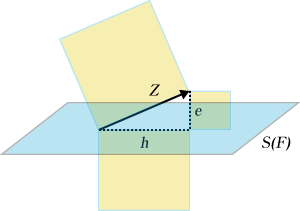
図2
因子分析結果の読み方
因子分析で得られる指標
因子負荷量
直交解を求めた場合に限りますが各変数と各因子の相関を表します。その場合は因子負荷量は、相関係数なので0から±1の値をとります。バリマックス回転が直交解の方法としてよく利用されます。
しかし、次の項の共通性の推定により、独自因子の情報は共通因子空間から除かれていることに注意してください。通常、この因子負荷量が高い変数を考慮して、因子の名前をつけます。
共通性
各変数が因子空間で表される分散を表しています。0から1の値をとります。
これも直交解を求めた場合に限りますが共通性は、各因子負荷量の2乗和となります。
寄与率
ある因子がどの程度の説明力を持っているか割合を表します。
独自因子の割合=独自性です。Uniqueness と言います。
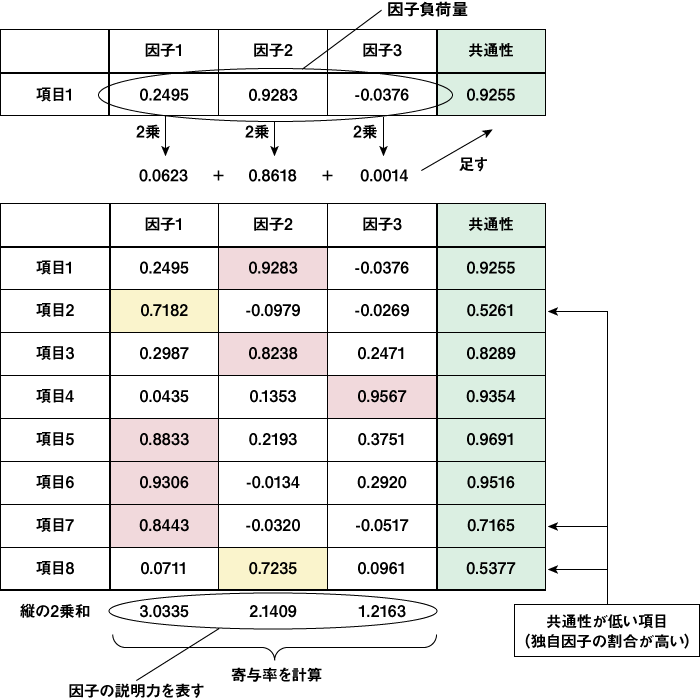
図3
因子得点
因子得点は、各因子ごとの各個体(対象者)のスコアを表します。因子得点が高い人は、その因子に影響されている度合いが高いといえます。
下記の表は、適性検査の成績を因子分析した結果の一部です。「計算能力」、「図形処理能力」、「言語能力」、「記憶能力」という4つの因子が抽出され、対象者ごとの因子得点を求めたものです。因子得点から、対象者を3つのグループに分けることができました。
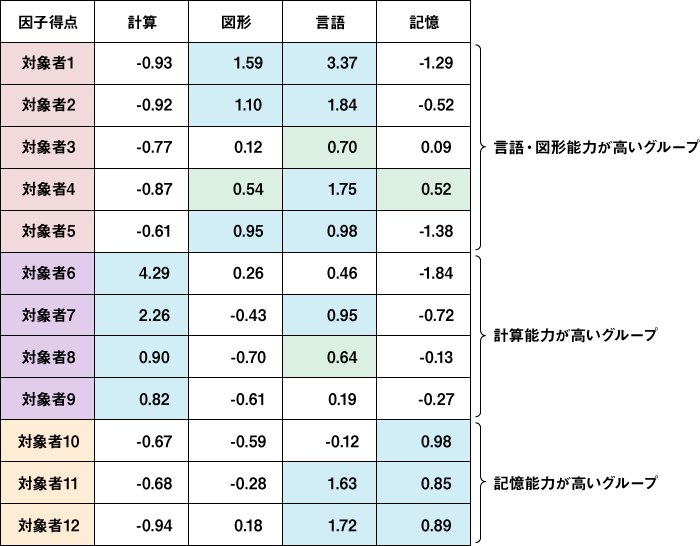
図4










