回帰分析
回帰分析のモデルと基本式
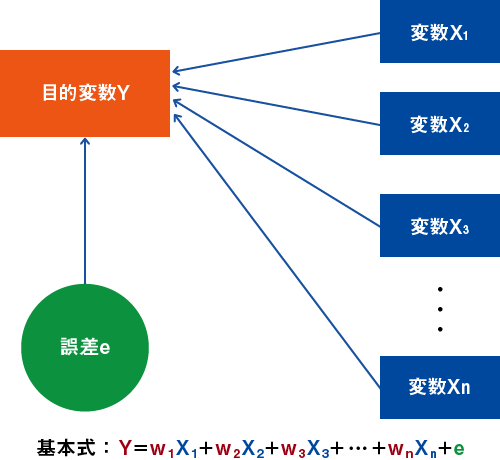
1つ(単回帰分析)または複数(重回帰分析)の説明変数と、1つの目的変数の関係を求め、説明変数から目的変数を推定します。
回帰分析の例
例としてある店の顧客に対する販売実績と、顧客の属性の関係を分析します。目的変数として、ある年の各顧客の購入額をとります。説明変数として、顧客の属性(年齢、性別、家族人数、年収など)を用いることとします。すなわち、
購入額=定数+ a ×(年齢)+ b ×(性別)+ c ×(家族人数)+ d ×(年収)+(誤差)
※性別などの名義尺度は数量として扱えないため、男性=1、女性=0といったダミー変数を与えて分析します。
という式において、a,b,c,d(これを偏回帰係数といいます)の値と定数を推定します。求め方は、最小二乗法または最尤法が用いられますがその理論の説明は省略します。その結果、求められた式、例えば、
購入額の予測値=5,000+30×(年齢)+300×(性別)+450×(家族人数)+0.001×(年収)
などという関係式が得られるのです。これを回帰方程式と呼びます。この式に新しい顧客の属性データを入れれば、購入額が推定できるというのが、重回帰分析の考え方です。
一方、この関係式において、説明変数(属性)が、購入額(目的変数)に対しておよぼす影響の大きさを知りたいということがよくあります。上の関係式では、年齢や年収は単位が違います。したがって年齢の項の偏回帰係数30と年収の項の偏回帰係数0.001は直接比較できません。そこで、あらかじめ説明変数を平均0、分散1に標準化()しておくと、単位が同一の条件下で分析できます。
このように、説明変数を標準化して求めた偏回帰係数を標準偏回帰係数といい、この標準偏回帰係数の大きさで、説明変数の説明力(目的変数への影響の大きさ)を比較できます。ただし何%のウェイトを持つというような、数量的な評価はこのままではできません。
回帰分析モデルの評価
重相関係数と決定係数
重相関係数とは、1つの目的変数と、その予測値との相関を表わすものです。すなわち、さきほどの例では、目的変数である実際の購入額と、重回帰分析式で求めた予測値の相関を表わします。したがって、当然、この重相関係数(rと表わすことが多い)が1に近いほど、重回帰分析モデルが購入額をよく表わしていることになります。
また、この重相関係数(r)の2乗を、決定係数(r2)といいます。決定係数は、基準変数の分散に占める予測値の分散の比率を意味するので、重回帰分析の精度を表す指標としてよく用いられます。
説明変数の選択
実際に重回帰分析を行う場合、説明力が高い少数の説明変数で、適合度の高いモデルができることが理想です。説明変数の選択方法には、
- 強制投入法(すべての変数を説明変数として重回帰式を作る)
- 変数増加法(変数のない重回帰式に、新たな変数を追加しては、評価していく)
- 変数減少法(全変数を入れた重回帰式から、1つずつ変数を減少させて、評価していく)
- ステップワイズ法(変数増減法)
などがあります。
ステップワイズ法は、最も代表的な説明変数の選択方法で、1つずつ説明変数を、入れたり除いたりしながら、だんだんと効率のよいモデルに近づけていくやり方です。
多重共線性(マルチコ)
重回帰分析で注意すべきことは、本来説明変数間は独立であるべきという仮定です。説明変数A、B間に高い相関関係があると、偏回帰係数の推定精度が極端に落ちます。これを、多重共線性(正確にはマルチコリニアリティ)といいます。いわゆるマルチコは俗称です。多重共線性は、ステップワイズ法の過程で偏回帰係数の符号が次々と逆転することなどによって発見することもありますが、説明変数間の相関行列をもとにCNと呼ばれる指標を求めて発見することができます。
なお、共分散構造分析(SEM)を用いれば、相関の高い変数AとBを一つの潜在変数の測定変数としてモデリングすることで多重共線性の問題を回避できます。








