判別分析
判別分析は、個体（対象者）の特性（回答データ）から、その個体（対象者）がどの群に属するかを判別する手法です。
判別分析の原理
判別分析は、重回帰分析における従属変数が、カテゴリーになったモデルだといえます。例えば、下図のように判別対象が2群の場合、予測される変数が0か1の2値データになったものと考えられます。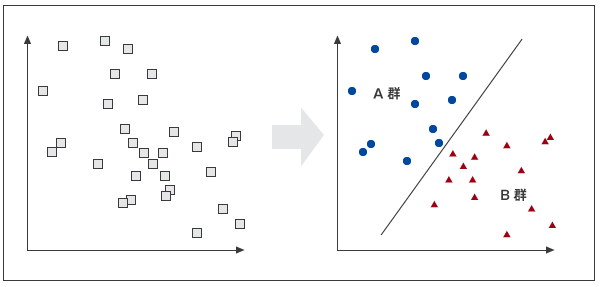
要約すれば、判別分析は、従属変数が質的変数で、説明変数は量的変数の（重）回帰分析（線形判別関数を使う場合）ともいえ以下の通りに判別します。
直線で仕切る（線形判別関数）
Z = W1X1 + W2X2 + W3X3 + ・・・ WnXn + a0（a0：定数）で、Z＞0かZ＜0かで判断します。上式は、重回帰分析の式と同じ形をしています。実際に、従属変数を1または0の値を与えて重回帰分析を行うと、偏回帰係数と線形判別関数の判別係数ｗは一致します。
判別分析の適用事例
判別分析は、他の多くの多変量解析手法のように集団の情報を得るためというより、個人（個体）を分類する目的で使われることが多いといえます。例えば、以下のような場面で用いられます。- セールス効率化のために、見込み顧客を“購入しそうな顧客”と“購入しそうにない顧客”に分ける
- 現在の顧客をカテゴリー分けする場合の資料に使う
- クレジットの申込み者に対する与信（クレジットカードを発行するかどうかの決定資料）とする
- 検査結果から、疾病の有無を判断する
判別分析は、説明変数が量的変数の場合に用いられますが、説明変数が質的変数の場合は、数量化2類を用います。
