
集まるデータを分析して購買や解約に至る要因を推定する場合、重回帰分析に代表される多くの分析手法は図1左図のように複数の説明変数Xから並列的に目的変数Yを予測・説明するモデルである。一方で図1右図のように説明変数間の複雑な因果関係や関連構造を想定してYを説明する柔軟なモデルが作れれば、より情報量が多く、説得力の高い分析ができるだろう。これを実現するための分析手法として、今回は「ベイジアンネットワーク」を紹介したい※1。
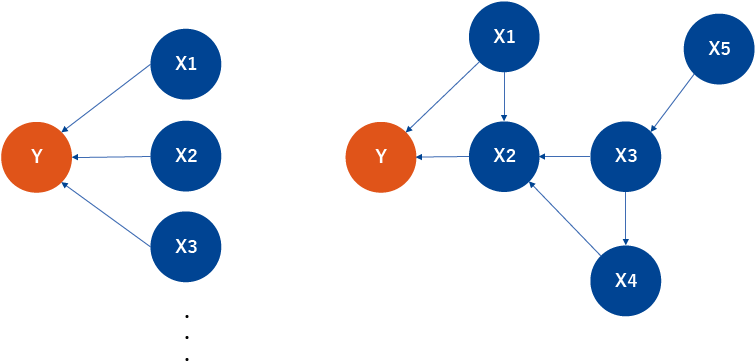
図1
ベイジアンネットワークでは、事象を図1のXやYのようにノードで表し、事象間を一方向の矢印で結合していくことで、複雑な事象間の関係をわかりやすく整理・把握する※2。事象A→事象Bの関連はベイズ統計の考え方を利用して、事象Aの事前確率と事象Bで確認されたデータ(証拠)から事象Bの事後確率を順次計算していく。出来上がったネットワークを見るだけでも複雑な変数間(事象)の関係性を把握できるが、さらにネットワーク上の一部の事象データを更新させると、各事象の確率も更新されるので、様々なケースを想定したシミュレーションが行えるのだ。
とはいえ、実際に手元にある“集まるデータ(多変量データ)”から複数の変数の関係性を見つけ出して、図1右図のようなネットワーク図を構築するのは簡単ではない。また各事象(ノード)にはCPT(conditional probability table)という条件付確率表を割り当てなければならないが、実際の多変量データからこれを算出するのも大変手間がかかる。実務上は、専用のソフトウエアを使ってこれらの作業を自動的に行うことになる。
ベイジアンネットワークを構築してみよう
分析の様子をイメージしやすいように、サンプルデータを使ってベイジアンネットワークを構築し、CPTを算出し、シミュレーションをしてみよう。今回は表1のような6つの変数を含む架空の通信キャリアの1,000名分の顧客データから、解約を説明するベイジアンネットワークモデルを構築する※3。
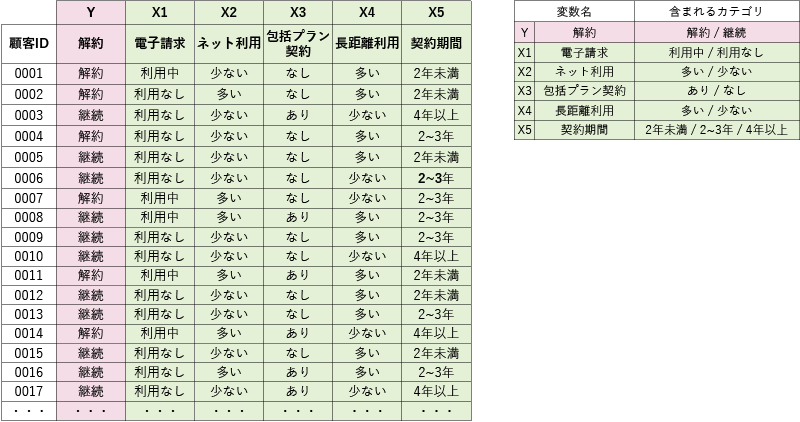
表1 分析に使うサンプルデータの内容
表1のデータから図1右図のようなネットワーク図を作る場合、考えられるネットワーク図の組み合わせは変数の個数がわずか6つであっても(Y(解約)からは矢印は発しないなどの制約条件を付けたとしても)、膨大な数になる。そのすべてを試行錯誤するのは手作業では困難であるが、組み合わせ探索プログラムと、候補となるネットワーク図が実データと適合しているのかを測定する指標(ネットワークスコア)を算出することで、効率的にデータに適合する最適なネットワーク図を見つけることができる※4。
探索・分析の結果、6つの変数から図2のようなベイジアンネットワークが構築された。また各ノードのCPTは表2のように算出された。
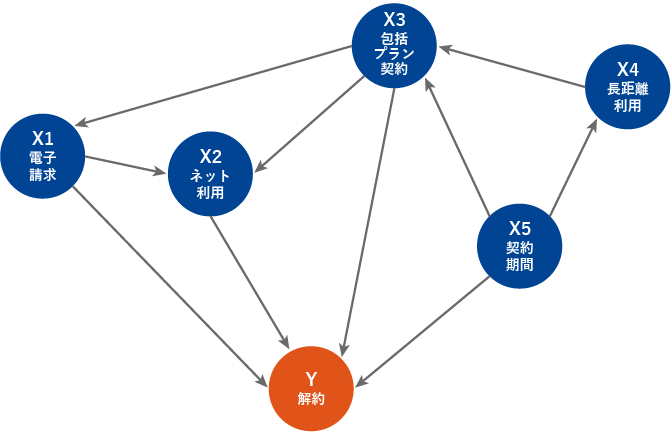
図2 構築されたベイジアンネットワーク
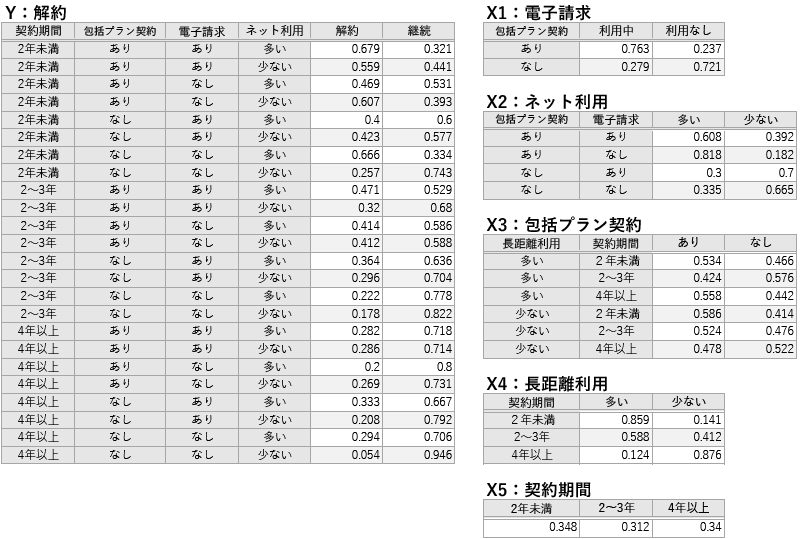
表2 計算された各ノードにおけるCPT
図2を見ると、解約に直接的に影響しているのは、直感的にも関係がありそうだと想像できる契約期間の長さだけでなく、電子請求の有無、ネット利用の多さ、包括プラン契約の有無も要因であるとわかる。長距離通話の利用状況は契約期間からの影響を受けた上で、包括プランに契約しているかどうかを介して解約に影響を及ぼすという構造も見て取れる。元データから変数間の関係性を抽出し、図2のようなネットワーク図を探し出せるところにベイジアンネットワーク分析の威力を感じるだろう。
ベイジアンネットワークを使ったシミュレーション
続いて今回の分析で得られたネットワーク構造と各ノードのCPTをコンピューターに登録し、シミュレーションを行っていこう※5。それらを基に計算された各ノードの事前確率は図3の通りである。
ベイジアンネットワークでは図3にある初期状態の事前確率が、各ノードの条件を変更した場合(=各ノードにデータという証拠が得られることに相当)にどのように変化していくのかを再計算し、事後確率として出力する。これはベイジアンネットワークの性質を利用したシミュレーションを行うことに他ならない。例えば図3において、解約ノードに「解約」という条件を設定してみると(解約したというデータが得られたと考え、解約=100%、継続=0%とする)、各ノードの確率が再計算され、事後確率に更新される。図3と図4を比べてみると、解約という条件を設定したことで各ノードの一部のカテゴリの確率が上昇している。それらを読み解くことで、電子請求=利用中、ネット利用=多い、包括プラン契約=あり、長距離通話利用=多い、契約期間=2年未満、という要因(カテゴリ)が、解約に影響しているとわかるのである。
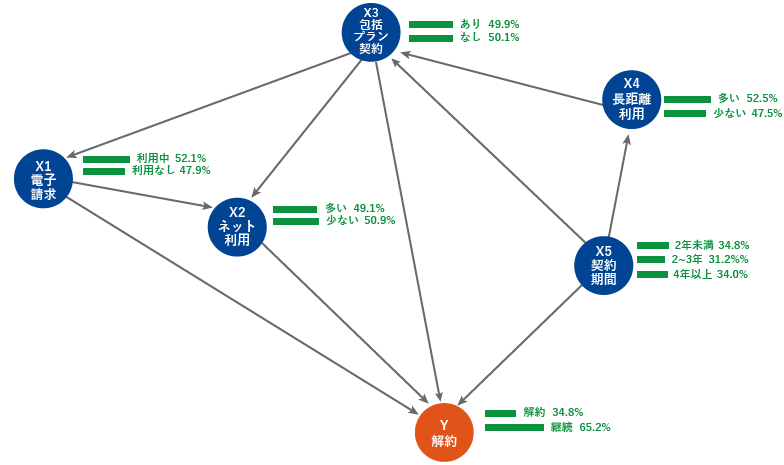
図3 構築したベイジアンネットワークの事前確立(初期)
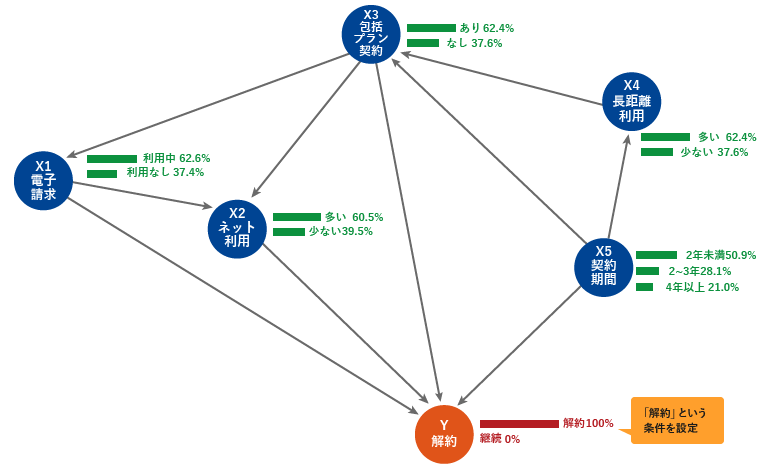
図4 「解約」というデータから得られた場合の各ノードの事後確率
あるいは、もともと4年以上契約の場合の解約率は21.5%(図には記載していない)と全体に比べ低く推定されるが、図5のように契約期間=4年以上、包括プラン契約=なし、という条件を設定してみると、さらに解約率は16.5%まで下がると予測される。包括プランはあまり利用しない無駄なプランも含まれているから長期利用者の評価は低いのかもしれない。契約期間=4年以上に設定したうえで、解約以外の各ノードの条件を色々変えてみたところ、長距離通話利用の多い・少ないは解約率にあまり変化を及ぼさないが、包括プラン契約のあり・なしや、ネット利用の多い・少ない、電子請求の利用・利用なしは、条件次第で大きく解約率が変わることが、PC上でシミュレーションすることで一目瞭然になった。
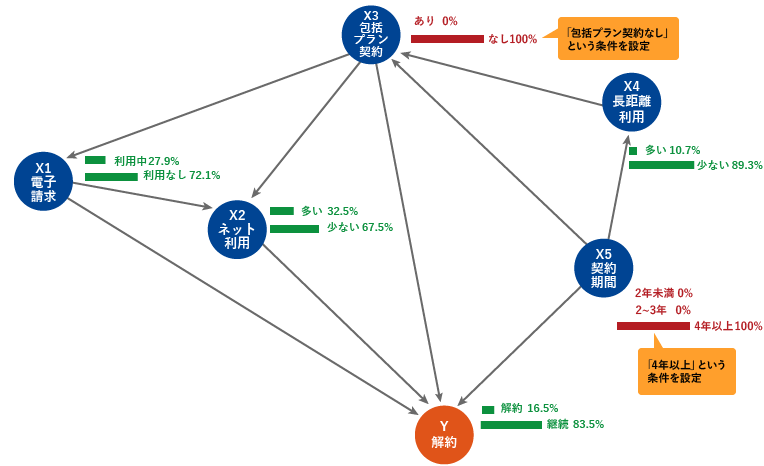
図5 「4年以上」「包括プラン契約なし」という条件を設定した場合の各ノードの事後確率
このようにベイジアンネットワークは、企業内に蓄積されている集まるデータから変数間の関係構造を浮かび上がらせ、要因推察や施策立案のヒントになるだけでなく、実際に様々な条件を変えてシミュレーションすることで、将来の予測にも役立てることができる。マーケティング実務の世界でも利用価値が大きいと言えるだろう。
※1:共分散構造分析(SEM)も図1右図のような変数間の構造を分析できるが、分析者が仮説に基づいてパス図を規定する必要があることや、完成したパス図を基に様々な条件を変えてのシミュレーションが行えないなど、ベイジアンネットワークに比べると使いづらい点がある。
※2:確率計算の一貫性を保つため、矢印をたどっていってもループ(循環)しないように矢印を引くことが求められる。
※3:サンプルで用いるデータはいずれの変数もカテゴリカルデータ(離散値)である。ベイジアンネットワークは連続値でも構築可能だが、連続値の場合は確率分布を考える必要があり、結果の読み取りが難しくなるため、できる限りカテゴリカルデータに変換して行った方が良いだろう。
※4:ここでは分析ツールRのdealパッケージを使用した。
※5:シミュレーションは機械学習フリーソフトWekaで行った。Wekaでは各ノードの条件を設定することで、各ノードの確率が動的に再計算されて表示されるので、様々なシミュレーションが手軽に行える。
渋谷直正著 連載『集まるデータ』のマーケティング活用術
著者の紹介
渋谷 直正
株式会社デジタルガレージ 執行役員 CDO(チーフデータオフィサー)
2002年に日本航空株式会社に入社。JALホームページのログ解析や顧客情報分析、航空券などのレコメンド施策の立案・企画・実施を担当。2014年、日経情報ストラテジー誌による「データサイエンティスト・オブ・ザ・イヤー」受賞。2019年より現職、デジタルガレージグループでのデータ活用を統括・推進する。ビジネスアナリティクスや実務に役立つ分析手法に詳しく、データを使ったマーケティングを得意とする。総務省統計局講座や大学での講演・記事掲載など多数。
著者の人気記事
カテゴリー
アクセスランキング
コラムランキング
メールマガジン
マーケティングに関するホットな話題やセミナーなどの最新情報をお届けします
