階層クラスター分析

階層クラスター分析のアルゴリズム

階層クラスター分析のためのアルゴリズムは複数存在します。実際はそれらの中から、データの特性に最も相性のよい手法を選んで分析を進めていきますが、ここでは最もシンプルな「最短距離法」を例に、階層クラスター分析の基本的な考え方を解説します。

図1のように散布図に描くことができるデータを、階層クラスター分析によって分類します。

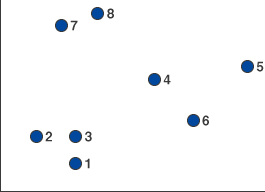
図1

まず全てのペア間の距離を求めます（図2）。そして、最も距離が短いものを最初に結合します。ここでは、距離が最も短い2と3を結合し、クラスターとします。

図2

2と3を結合してクラスターとしました。

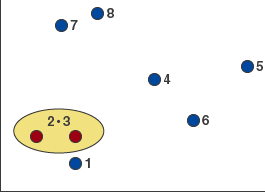
図3

次に2と3のペアを除いて、最も近いペアを探します。1と3です。

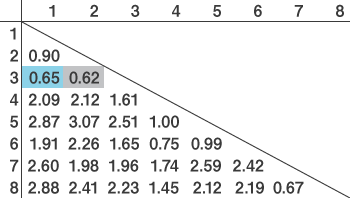
図4

3はすでに2とクラスターを形成しているので、1を2・3のクラスターに組み込みます。1・2・3がクラスターを形成しました。

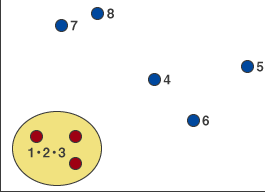
図5

ここまでの結合の過程をデンドログラムに表わすと図6のようになります。デンドログラムの縦軸は距離となっており、2つのグループが結合した距離のところで線分が結合するようになっています。今回2と3は0.62の距離で、1と2・3グループが、0.65の距離です。

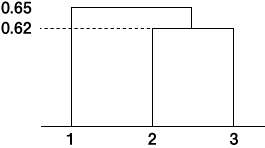
図6

次に近いペアは7と8なのでこれを結合します。

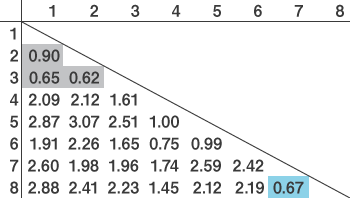
図7

クラスターができ、図8のようになりました。さらに、同様に進めていくと、次には3・4・5が1つのクラスターとしてまとまります。

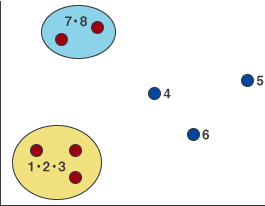
図8

4・5・6を結合し、クラスター分けができました。しかし、階層クラスター分析は、データ全てが1つのクラスターとしてまとまるまで、結合を続けます。

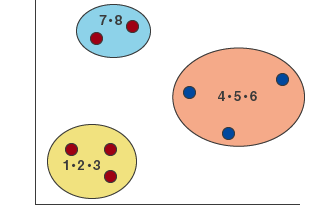
図9

すでに同じクラスターになっているペア間の距離（表のグレーの部分）は除いて、最も近いペアは4と8です。よって、3を含む4・5・6のクラスターと、8を含む7・8のクラスターが結合します。

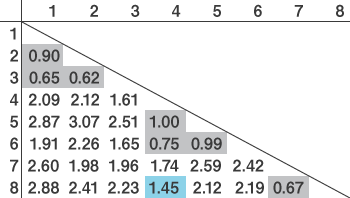
図10

次のステップで、1・2・3が4～8のクラスターに組み込まれ、階層クラスター分析は終了です。このような形で、全てのデータが1つのクラスターとしてまとまるまで結合を繰り返します。

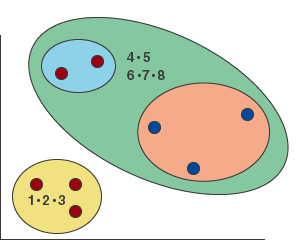
図11

最終的なデンドログラムは図12のようになります。

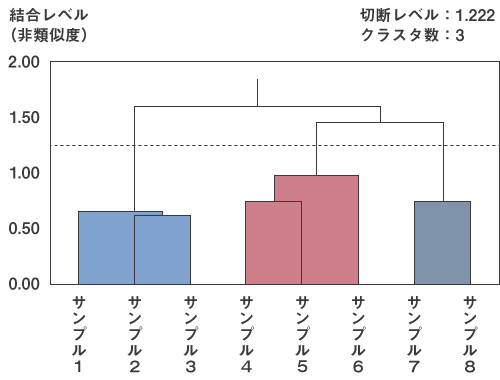
図12

より深く知りたい方はこちら（関連リンク）