非階層クラスター分析

非階層クラスター分析のアルゴリズム

非階層クラスター分析のための手法は複数存在します。ここでは最もポピュラーな手法であり、マクロミルでも採用しているk-means法のアルゴリズムを紹介します。

ある集団を、身長と体重という2つの変数を基準にして、3つのクラスターにk-means法で分類します。

使用するデータは図1にプロットされています。非階層クラスター分析では、まず事前に分割したいクラスター数を入力する必要があります。

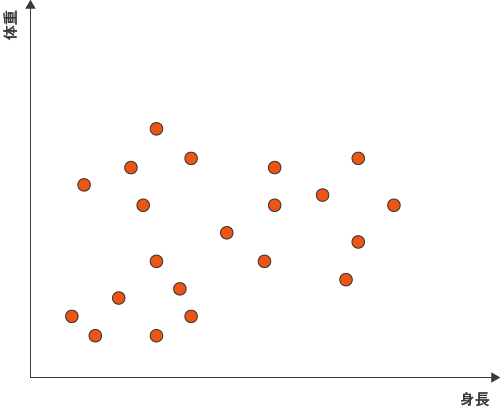
図1

今回のクラスター数は3です。サンプルの中から分割したいクラスター数と同じ、3つのサンプルをランダムに選び出して水色で表示しました。この3つのサンプルはシード（seed=種）といい、それぞれのサンプルと3つのシードに対する距離を計算して、最も近いシードを求めます。そして、仮に、それぞれのサンプルを最も近いシードと同じクラスターに属すると決めます。

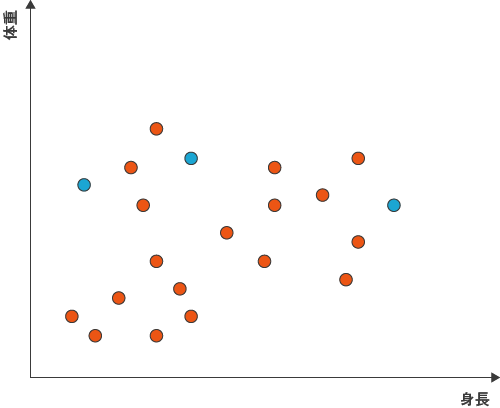
図2

このようにオレンジ、水色、黄色の3つのクラスターを仮につくることができます。しかし、これでは明らかにクラスター分けされているとはいえません。非階層クラスター分析の目的は、同じクラスターの中に属するサンプルはなるべく似通っているように、異なるクラスターに属するサンプル間ではなるべく違いがはっきりするようにすることです。

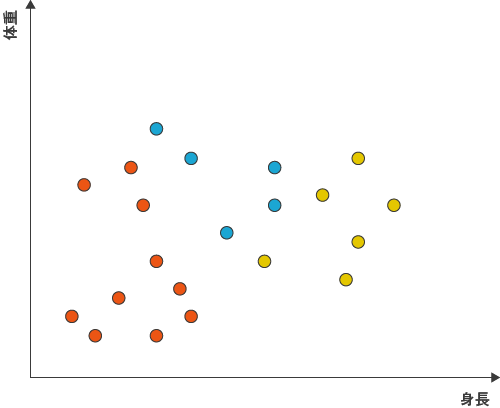
図3

そこで、3つのクラスターの重心をそれぞれ求めます。重心は、各クラスターの平均値をもとに算出します。オレンジのクラスターの重心をもとめるには、オレンジのクラスターの平均体重・平均身長をもとめます。3つのクラスターからもとめられた重心をひし形で表しました。

図4

次にこの重心を新しいシードとして、最初と同様にそれぞれのサンプルを最も近いシードと同じクラスターに属するよう、仮にクラスター分けします。2度目のクラスター分けの結果を示しました。オレンジのクラスターの2つが水色に、水色のクラスターのうちの1つが黄色のクラスターに移動しました。

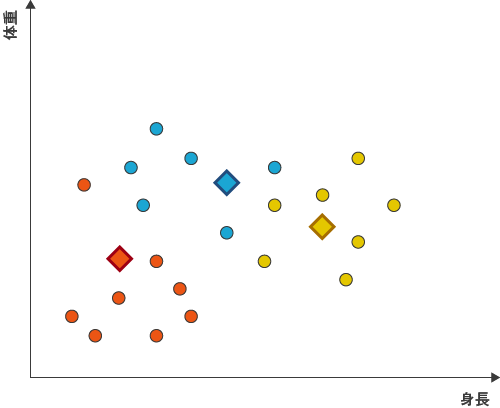
図5

前ステップでもとめた新しいクラスターをもとに、新しい重心を求め、クラスター分けをし直しています。前ステップで図の上の方にあるサンプルを失ったオレンジのクラスターの重心が多少下方向に移動し、そのためさらにもう1つのサンプルを水色のクラスターに取られていることがわかります。

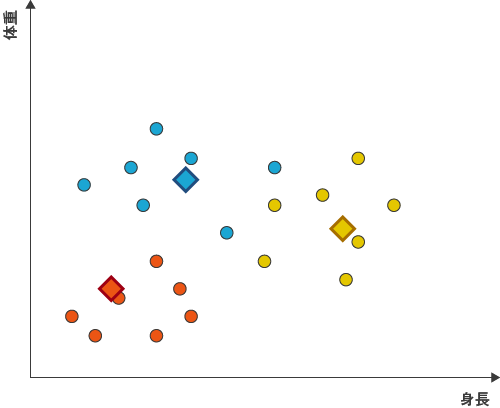
図6

また同じことを行ないます。水色のクラスターがオレンジのクラスターから左方向のサンプルを獲得したため、重心が左に移動し、黄色との境界線上のサンプルを失いはじめました。

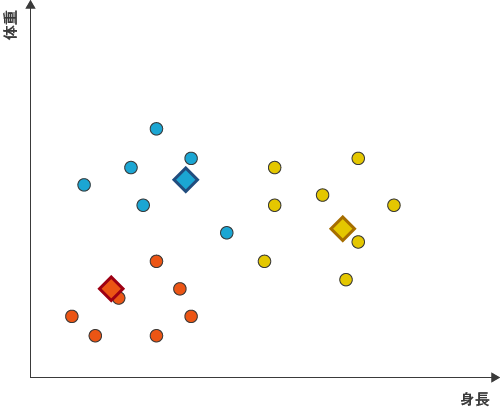
図7

水色の重心がさらに右側へ移動し、もう1つのサンプルを黄色のクラスターに取られました。この時点できれいに分かれているように見えますが、実際いままで繰り返したステップをこれ以降何度繰り返しても、これ以上クラスターに変化はありません。

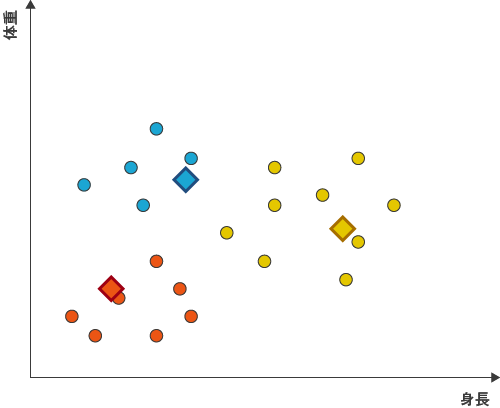
図8

このように、重心をもとめ、クラスタリングをしなおすという手法を繰り返せなくなるまで続けることがk-means法の考え方です。

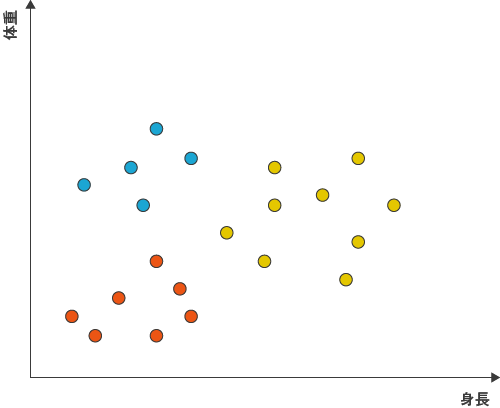
図9

より深く知りたい方はこちら（関連リンク）

クラスター分析 ＞＞

階層クラスター分析 ＞＞