コレスポンデンス分析
コレスポンデンス分析（コレポン、対応分析）とは、自社と競合他社など複数ブランドのポジションの違いを可視化する分析手法です。
コレスポンデンス分析の考え方
コレスポンデンス分析は、数量化3類と数理的には同じ手法です。
コレスポンデンス分析の基本の考え方は、行列（分割表）において、行項目と列項目の相関が最大になるように、行と列のカテゴリにスコアを与えることです。この場合の行列は、データシート、クロス集計表など、第1行（表頭）と第1列（表側）に注目する項目があり、他の部分にこの項目に対応するデータがあるものであれば何でもかまいません。相関が最大になるように並べ替えるということは、クロスセルにあるデータを見ながら、近い項目が隣り合うように並べ替えるということです。
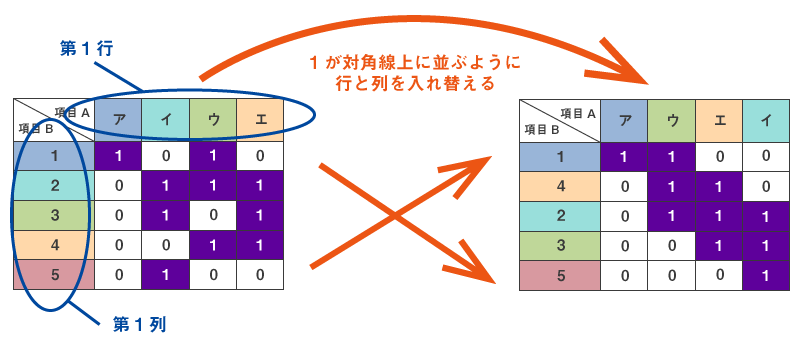
0と1の2値データで説明します。下左図のような行列があったとします。ここで、項目AとBは、対象者でも集計単位（性・年代など）でも質問項目でも回答カテゴリでもかまいません。下左図の1のセルがなるべく対角線上に並ぶように、行と列を入れ替えます。その結果が下右図です。 項目AとBをこの順番に並べたことで、項目AとBの相関が高くなったといえます。
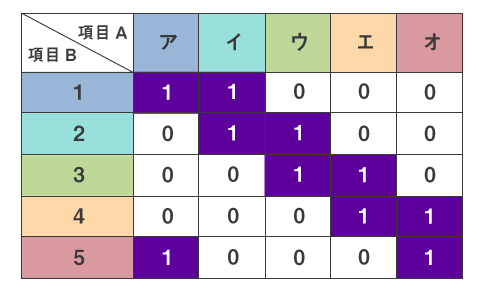
もちろん実際は、このようにうまく対角線上のデータが集まるとは限りません。例えば、下記のような場合は、どう並べ替えてもデータは対角線上に集まらず、1軸だけではデータを説明できません。したがって、データを説明するために、順次第２軸、第３軸、……と解を求めることになります。その際、第２軸は第１軸と直交するという条件下で定められます。さらに第３軸は第１軸、第２軸と直交するという具合に進んでいきます。最大の軸数は行数がｎ、列数がmとするとMin{n-1,m-1}です。
いろいろなコレスポンデンス分析
コレスポンデンス分析は適応範囲が広い分析法です。扱うデータも0、1のカテゴリデータだけでなく、頻度でもかまいません。
したがって、ローデータからでもクロス集計表からでも分析ができます。例えば、下記のような個人別データも、行列の形になっていれば分析可能です。ただしこの場合データは、あてはまる、あてはまらないなどの2値データを使います。
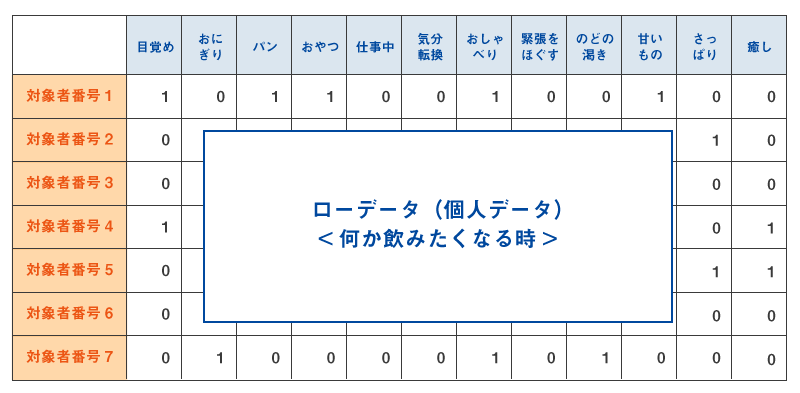
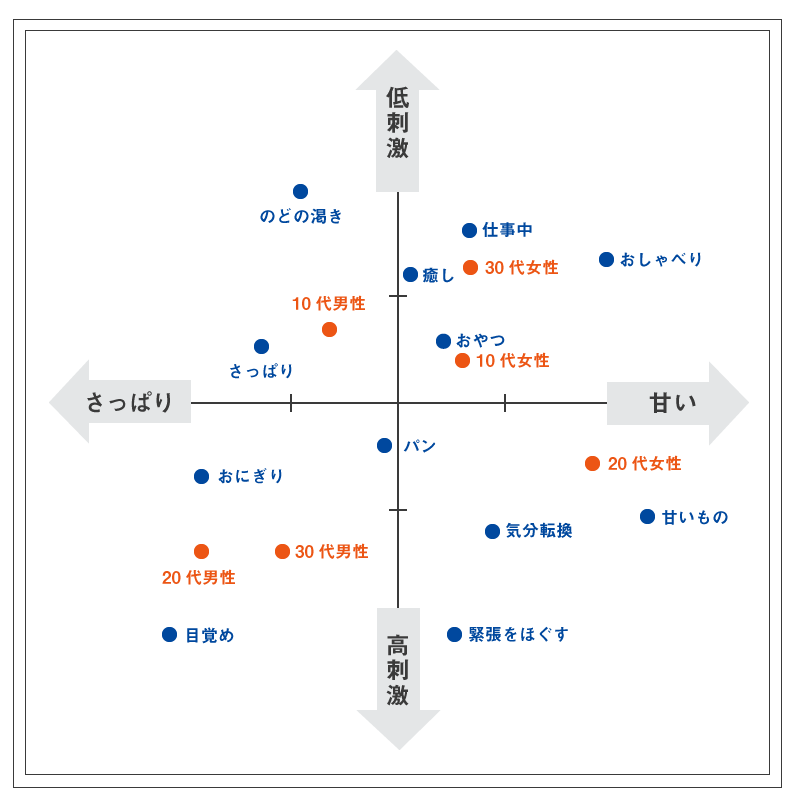
また、下記のように性・年代別に集計したクロス集計表から分析すると、表頭項目と表側項目を1つの図にプロットして比較することができます。
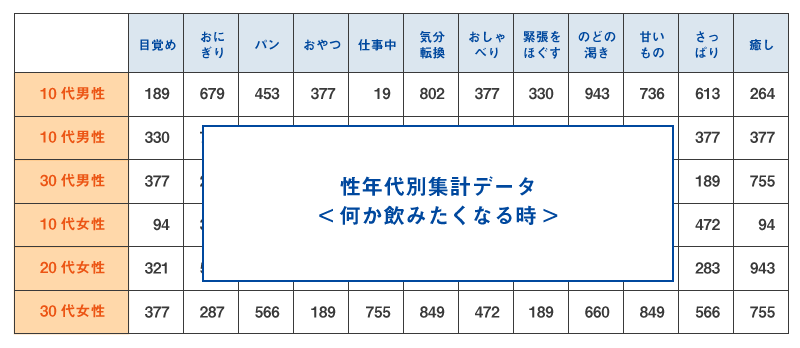
さらに、下記のように設問項目間のマトリクスを使うと、例えばブランドや商品とそのイメージやベネフィットを1つの図にプロットして比較することができます。
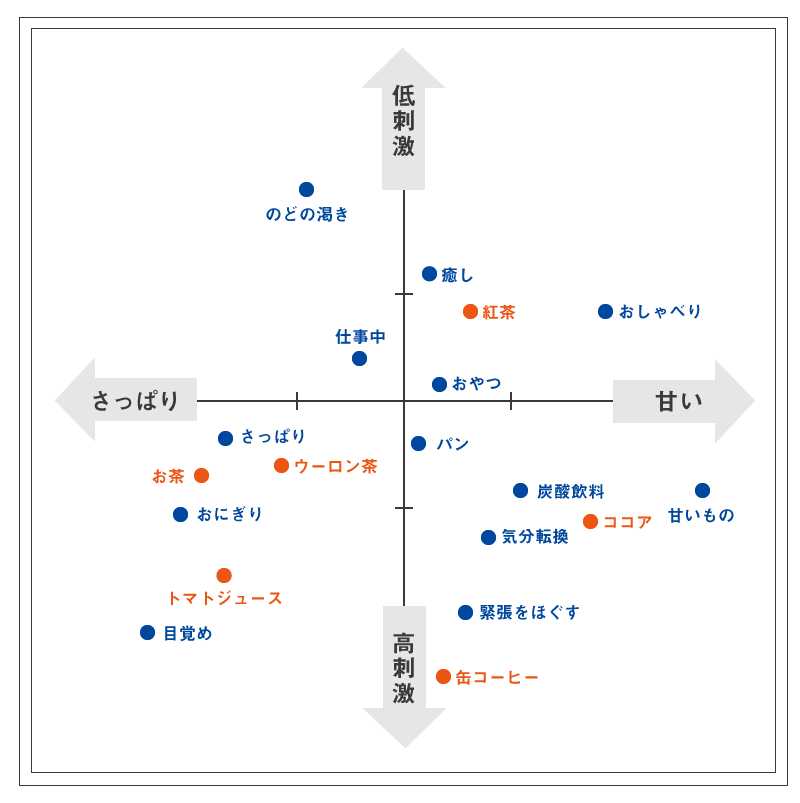
このような分析は、ブランドイメージの分析などで頻繁に用いられます。ただし、結果を読む際は下記の点に注意する必要があります。
- 軸に意味づけをした方が、結果の解釈がしやすい。
- 関連の強いカテゴリは近くに、弱いカテゴリは遠くにプロットされるが、これはあくまでカテゴリ間の相対的な関係で、絶対的なボリュームを表わすものではない。
- 縦軸の目盛りと横軸の目盛りはあわせた方がよい。そうしないと距離を見誤ることがある。
- ただしこのとき、縦軸と横軸の選んだ軸の固有値（あるいは寄与率）に注意する必要がある。
- クロス集計表から作成しているので、サンプルサイズは結果に反映されない。サンプルサイズが少ない際には注意が必要。（ブランドイメージを質問するときなど、認知者だけに質問すると、ブランドごとのサンプルサイズが異なるので注意する。例えば、Aブランドは認知者が10人で、5人が「はい」と答えて50％、Bブランドは認知者が100人で、50人が「はい」と答えても50％で、この差は結果に反映されない。）
- 異なる項目、例えば前の例では、飲料と飲用シーンのカテゴリの位置関係は、原点からの方向で判断する。原点から見て同じ方向にあれば、一見距離があっても、同様の意味づけが可能である。
- お客さまの課題・ニーズを伺って
リサーチの企画・提案を行います。 - 各種資料・調査レポートのダウンロードもこちらから
