二変量解析

二変量解析とは

二変量解析とは、一変量解析が１つの項目だけを対象にしていたことに対し、「身長と体重」、「年収と預金高」など2つの項目を対象とするものです。この二変量解析のデータを平面上にプロットしたものを散布図と言います。2つの項目を図にプロットしてみると、その項目間の関係がよく分かります。

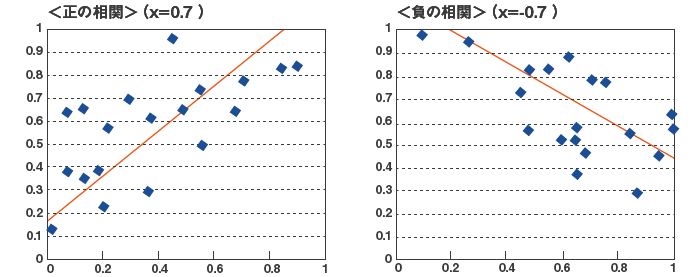
図1　相関のある分布

相関の強さを相関係数と言います。相関係数がプラスの場合は正相関、マイナスの場合は負の相関と言い、その絶対値が1に近い場合は相関が高く、0に近い場合は低くなります。

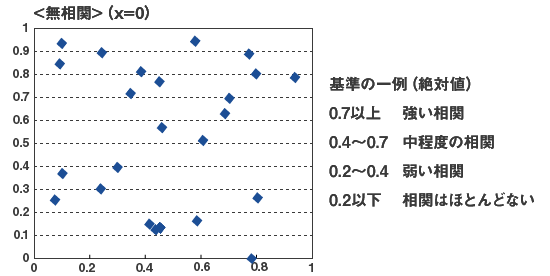
図2　相関のない分布

※本評価基準は実務的な慣用であり、理論的に根拠のある区分ではありません。

相関係数が低い（r=0.26）からといって、2つの項目に関係がないとは言えません。相関係数だけを見て解釈を行うと、2つの変数・事象には関係がないと言う間違った結論を出す危険性もあります。例えば、図3のようにケーキの甘さとおいしさの度合いの関係を見ると、ある程度までは甘くなった方がおいしいと感じるが、度を超えるとおいしくなくなります。

このような場合は、分析に工夫が必要となります。この場合は、相関係数にもとづく多変量解析をする際は、分析変数から除外するのが適切です。

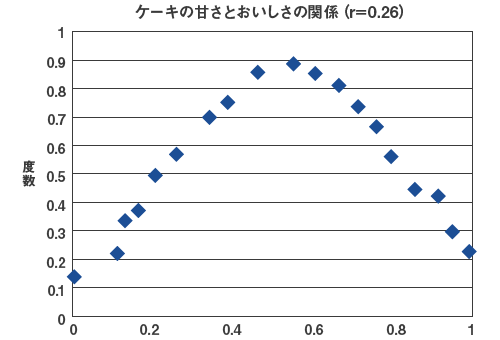
図3　相関がなくても関係のある分布

逆に、相関係数が高いからといって、単純にその2項目に因果関係があるとは限りません。身長と体重には高い相関があると想像できます。しかし、太れば身長も伸びるかと言えばそうではなく、相関関係と因果関係は異なります。

また、図4は小学生の漢字の書き取り成績とボール投げの距離の相関を見たものです。全体で見ると相関係数は0.83となり、高い相関がありそうです。しかしこのデータが小学校1年生と6年生のデータだった場合はどうでしょうか。小学校1年生（オレンジ）だけで見ると、相関係数は-0.12、6年生（青）では0.13となり、漢字の書き取りとボール投げの間に相関がないことがはっきりします。これは本来は層別すべき状況で、適切な層別が行われなかったために起こった現象です。

ここまで極端なケースでは無いとしても、実際の分析の場面において起こりがちな現象であるため、注意が必要です。

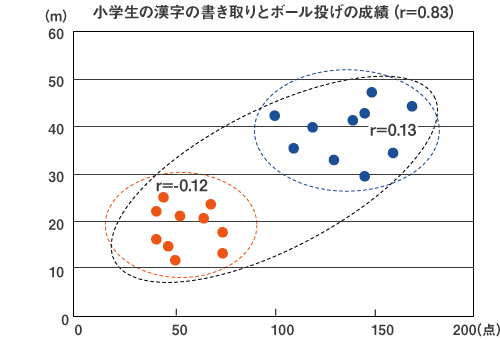
図4　層別すれば相関がない分布

より深く知りたい方はこちら（関連リンク）

多変量解析 ＞＞

一変量解析 ＞＞