
解釈性から見た予測モデルの違い
集まるデータを分析する数多の手法の中で、重回帰分析は最もメジャーな手法だろう※1。重回帰分析は過去の結果(正解)がわかっているデータから統計モデル(重回帰式)を作るのだが、それを行う目的は大きく分けると以下の2つである。
- (1)作ったモデルに、「結果が未知のデータ」を代入して予測値を求める(予測)
- (2)作ったモデルを解釈し、「どの変数が結果に効いているのか?」を探る(要因推定)
昨今のデータサイエンスブームの中では、予測には精度の高い機械学習系のモデルが使われることが多く、精緻な予測を行う目的で古典的な重回帰分析が実務で使われることは稀である。一方でモデルの中身を解釈し、結果に与える要因やその大きさを理解して知見を得たり、施策を考える際のヒントにしたりなど、(2)の要因推定の目的ではマーケティングの現場でも重回帰分析が広く使われている。古典的な手法であるゆえ、モデルの中味がシンプルかつホワイトボックスで解釈しやすい点が好まれているからである。
今回は重回帰分析を(2)の目的で使う際に、「どの変数がどれくらい効いているのか?」を直感的に示せる新しい手法を紹介する。
重回帰分析の結果の見方をおさらい
まずはサンプルデータを使った重回帰分析の結果を見ていこう。
表1は今回使ったサンプルデータで、20件の不動産中古物件の価格をY、それぞれの物件の広さ、築年数、最寄り駅までの時間をX1、X2、X3とした多変量データである。中古物件の価格(Y)を、(X1)(X2)(X3)の3つの説明変数を使って予測する(説明する)重回帰モデルを作った。
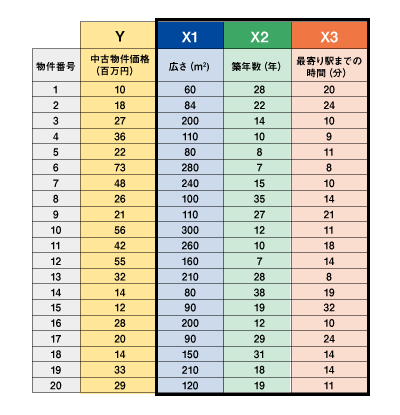
表1:今回重回帰分析に使うサンプルデータ
重回帰分析の結果は表2の通りである※2。分散分析表のp値を見ると0.05未満なのでこの回帰式は有意である。R2値を見てみると、3つの説明変数で、Yの分散の約73%を説明できていることがわかる※3。
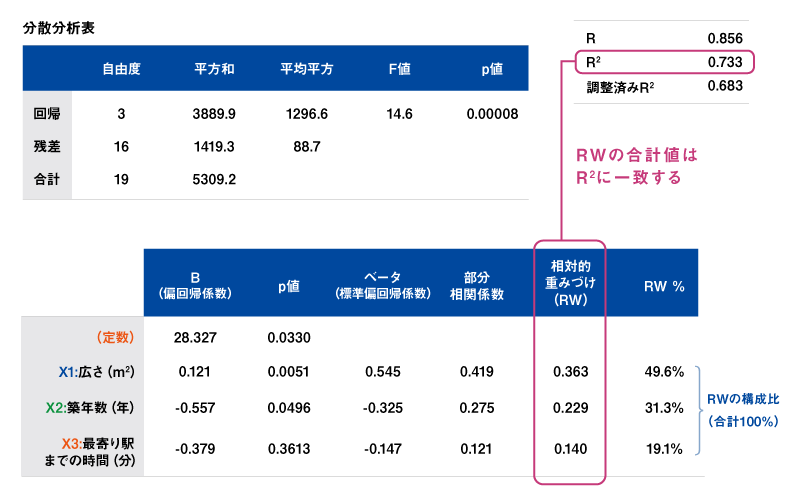
表2:重回帰分析の結果
続いて各変数のパラメータの推定値の表を見ていく。
この表が重回帰分析の解釈では最も重要である。3つの説明変数のB(偏回帰係数)の値を見ていくと、広さ(X1)の係数は0.121であるので、他の変数(X2とX3)の値を固定した場合、広さが1m2増えると、中古物件の価格が12.1万円上がると解釈できる。逆に築年数と駅までの距離の係数はマイナスであることから、中古物件の価格は1年古ければ55.7万円、駅までの距離が1分増えれば37.9万円安くなる※4。
それでは、3つの変数のうち、どの変数がもっとも中古物件の価格を予測するのに寄与しているのだろうか?
3つの変数は単位がそれぞれm2、年、分と異なるので、単純にBの大きさの大小では比較できない。そこでそれぞれの変数の大きさを調整して同じ尺度で比較できるベータ(標準化偏回帰係数)に注目する。ベータの絶対値を見ると、広さが0.545と最も大きく、次に築年数の0.325、最寄り駅までの時間は0.147となっている。各変数の中古物件価格への影響力の大きさをある程度知る目安になる※5。
各説明変数の目的変数への寄与の大きさを知るのは意外と難しい
以上が基本的な重回帰分析の結果の見方であるが、特にマーケターにとって興味があるのは、複数ある説明変数の中で、どの変数(要因)が目的変数に影響を及ぼしているのか、その影響の大きさを具体的な数字として知ることであろう。各説明変数が複数の代替案の判断材料になりうる場合などは、各変数の貢献度を定量的に把握したいニーズが出てくる。先に述べた通りベータを見ることである程度目安にはなるのだが、重回帰分析の場合、実はけっこう厄介な背景がある。
図1を見てほしい。ここでは目的変数Yに対し、2つの説明変数X1とX2を使って重回帰分析を実施した時の各変数の関係を示している。
Bやベータや部分相関係数はこの図の太線で囲った領域に相当する。この状態でX1、X2がYにそれぞれ影響を与えている寄与を見る場合、X1とX2に全く相関がない場合(つまり相関係数が0。これを独立という)は左図のようになりシンプルである。aやbそのもの(=ベータ)がそれぞれの変数の寄与分ということになる。
しかし実際のマーケティングデータは左図のようなことはほぼなく、少なからず説明変数間に相関が存在する。今回のデータでも、表3の通りX1、X2、X3には相互に相関がある。このようなケースでは図1の右図のようになり、重回帰分析の変数間の関係は複雑になる。
すなわちaやbだけ分かったとしても、X1とX2の両方が共通してYに影響を与える領域であるcの部分をX1寄与分とX2寄与分に分離できないため、Yに対するX1とX2のそれぞれの寄与分を示すことができないのである。
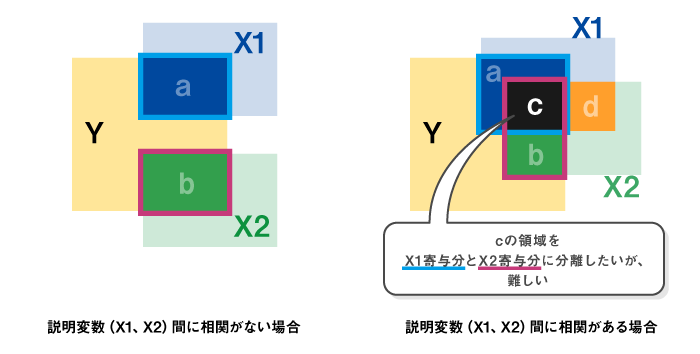
図1:重回帰分析のイメージ図
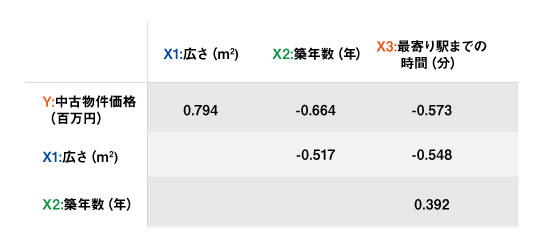
表3:各変数間の相関係数
相対的重みづけ分析(RWA)を使ってみよう
前述のような問題に対し、Yへの各説明変数の寄与の大きさを相対的な割合で示せる手法が相対的重みづけ分析(RWA:Relative Weight Analysis)である。
図1で言うと、cの領域をX1寄与分とX2寄与分に分離し、それぞれに(a、bからcを引いた)残りのaとbの領域を加え、Yに対するX1とX2の寄与分を数字で示せるイメージである。計算の詳細は割愛するが、RWAを実施すると、今回の例では、Yの分散をX1、X2、X3それぞれが何%ずつ説明しているのかを算出することができる。
具体的には表2のRWの列にあるように、それぞれの説明変数が説明するYの分散が算出され、この値の合計は今回の重回帰式で説明できるYの分散(つまりR2=0.7326)に一致する。X1~X3でMECEになっているので(ダブりがない)、それぞれの説明変数が説明できるYの分散の割合(内訳)も知ることができる(表2のRW%列の数字)。
この例では、広さが49.6%、築年数が31.3%、駅までの時間が19.1%(合計は100%)となり、この割合で中古物件価格に寄与していると解釈することができるのである(図2)。
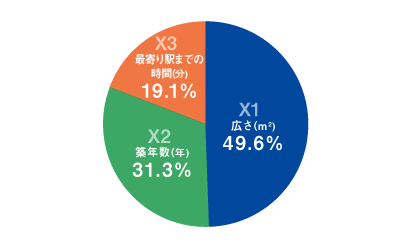
図2:各説明変数の、目的変数への寄与の大きさの割合
RWA※6はまだあまりなじみのある手法ではないが、各説明変数の寄与をMECEに構成比で示すことができ、直感的にも理解しやすく相手にも説明しやすいだろう。特に重回帰分析から知見を得たいマーケターには価値が大きい手法である。
* * *
これまで約1年半、9回に渡って「集まるデータ」のマーケティングでの活用法を紹介してきましたが、今回で最終回となりました。
長くご愛読いただきありがとうございました。
株式会社デジタルガレージ 執行役員 CDO
渋谷直正
※1:Excelにアドインされている分析ツールでも手軽に実施できるため、マーケターの中にも一度は分析した経験がある人も多いかもしれない。ただしExcelの分析ツールの回帰分析では、分析できる説明変数の数が16個までという制限がある。
※2:ツールによる違いはあるが、おおむねこのような数値が出力される。なお表2では説明上不要な出力は省略している。
※3:重回帰分析では説明変数が増えることによりR2が高くなる傾向があるので、調整済みR2値を参照することも多い。今回は比較的高いR2になっているが、実務では0.5以上あればまずまずのモデルと判断してよいだろう。
※4:p値の欄を見ると、広さと築年数は5%水準で有意であるが、駅までの時間は有意ではないことが分かる。実務では有意ではない変数は除去して改めて重回帰式を作ることが多いが、今回はそのまま3変数を採用する。
※5:ベータの正確な解釈は、「X1が1標準偏差だけ増えたときに、Yがβ標準偏差だけ増減する」であるが、あまりそういう解釈は行わず、X1~X3の相対的な寄与の大きさの目安程度とするのが一般的である。ベータはおおむね-1~+1の範囲内の数値となる。類似の指標として表2にある部分相関係数がある。部分相関係数とは、例えばX1の場合、X1を目的変数に、X2とX3を説明変数にして重回帰分析を実施し、その際に算出される残差とYとの相関係数である。直感的には、X1のうち、X2とX3で説明される部分を除去した残りの部分がYとどれだけ相関しているかを表している、と考えればよい。それぞれの説明変数“固有”の要素とYとの単相関を見ているのでイメージはしやすいが、せっかく重回帰分析をして他の変数との関連も含めたモデルを作っている価値は薄れてしまう。
※6:RWAは、分析ツールRのrelaimpoパッケージや、こちらのサイト で実行可能である。
渋谷直正著 連載『集まるデータ』のマーケティング活用術
著者の紹介
渋谷 直正
株式会社デジタルガレージ 執行役員 CDO(チーフデータオフィサー)
2002年に日本航空株式会社に入社。JALホームページのログ解析や顧客情報分析、航空券などのレコメンド施策の立案・企画・実施を担当。2014年、日経情報ストラテジー誌による「データサイエンティスト・オブ・ザ・イヤー」受賞。2019年より現職、デジタルガレージグループでのデータ活用を統括・推進する。ビジネスアナリティクスや実務に役立つ分析手法に詳しく、データを使ったマーケティングを得意とする。総務省統計局講座や大学での講演・記事掲載など多数。
著者の人気記事
カテゴリーから探す
タグから探す
アクセスランキング
コラムランキング
メールマガジン
マーケティングに関するホットな話題やセミナーなどの最新情報をお届けします
