
解釈性から見た予測モデルの違い
集まるデータなどから予測モデルを作り、例えば顧客ごとの購入確率の予測値を算出し、ターゲティング施策などに活用することは、データを使ったマーケティングの定石である。予測モデルには、古典的な線形回帰分析から、最新の機械学習技術の一種であるXGBoost※1など様々な手法があるが、モデルの解釈性という観点から見ると、ホワイトボックス型とブラックボックス型に大別される。一般に機械学習によるモデルの方が精度は高くきめ細かい予測が可能であるが、その反面、ブラックボックス型であるためどういう要素が予測に寄与しているのかを人間が理解するのは難しく、「理由は気にしないので、とにかく結果が当たる(=予測精度が高い)モデルが欲しい」という局面には適している。一方で本連載の第1回でも書いた通り、マーケティングには一程度の説明責任や顧客理解が求められるため、「当たりさえすればよい」という手法は使いづらいのも実態だ。
モデルの解釈性について、よりイメージしやすいように図1をご覧いただきたい。ここでのレバーはモデル構築に使用された変数(特徴量)を意味しており、ホワイトボックス型では、それぞれのレバー(変数)が何を意味するのかが明示されていて、さらにそれぞれのレバーをどれだけ動かせば予測値がどれだけ動くのかも明らかになっている。重回帰分析の偏回帰係数の値を見れば、その変数が1単位増えたときに予測値がいくつ増減するのかがわかるという例が典型である。それに対してブラックボックス型では、レバーがたくさんあり、しかもそれらは機械が作り出した数学的な特徴量であるため、その意味を人間が解釈することはできない。加えてそれぞれのレバーをどれだけ動かせば予測値がどれだけ動くのかも通常は示されない※2。つまり結果だけを信じて正解データと照合し、精度を確かめるしかないのである。
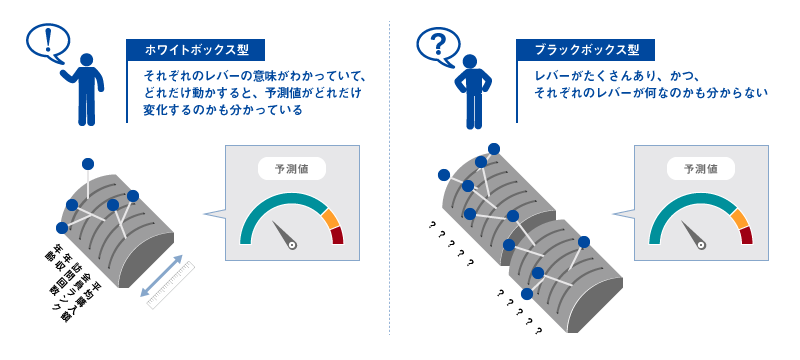
図1 予測モデルの違い(イメージ)
では、ブラックボックス型ではあるものの、せっかく精度が高い機械学習の予測モデルに解釈性を持たせることで、マーケティング施策に活用できる方法はないだろうか。
変数をいろいろと動かしてみることでブラックボックスの中味に迫る
機械学習で作ったモデルはいわば分類器であるので、各変数の値を様々に代入してみることで、予測値も様々に変化する。この特性を利用し、他のすべての変数の値を固定し、残った1つの変数について様々な値を代入して予測値の変化を調べてみることで、その変数が予測値にどれくらいの影響力を与えているのかを類推できる。すべての変数1つ1つについて同じことをすれば、相対的にどの変数が予測値の増減に貢献しているのかが浮かびあがってくる。
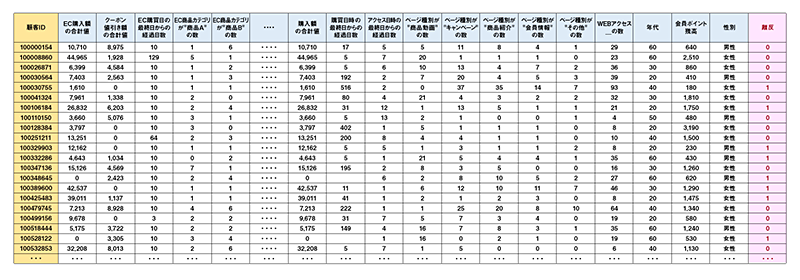
事例として、表1のようなあるBtoC企業の会員の継続/離反の正解データをもとに、離反確率を算出する予測モデルを機械学習で構築したケースで説明しよう※3。
予測モデルを作った後、投入した33変数すべてについて、他の32変数は値をそれぞれの変数の平均値に固定し、注目している1つの変数の値をいくつかに区切って検証していく※4。そのようにして33変数すべてを検証し、そのうちの1つである「会員ポイント残高」変数について結果を示すと図2のようになる。

※前のページへ戻るには、ウィンドウの画像が表示されていない部分をクリックするか、閉じるボタンを押してください
表1 会員離反予測モデル構築に使用したデータ(一部抜粋、架空データ)
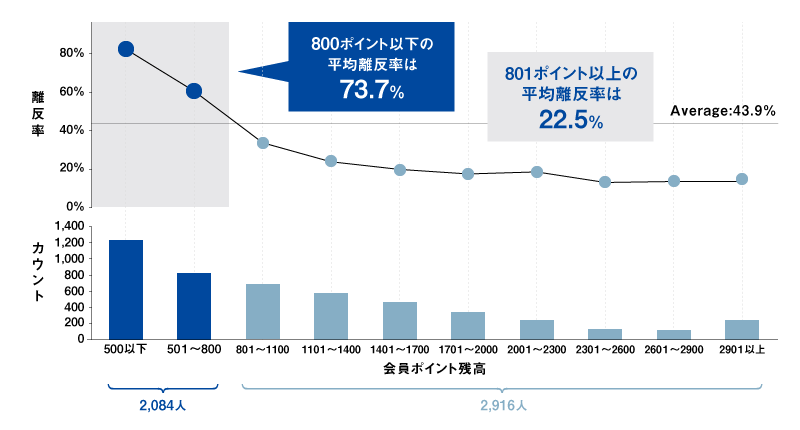
図2 変数「会員ポイント残高」の範囲ごとの離反率と顧客数
図2を見ると、会員ポイント残高の保有数が801ポイント以上のところから、離反率の低下が緩くなっていることがわかる。そこで、全会員を800ポイント以下の2,084人と、801ポイント以上の2,916人の2群(セグメント)に分けてみると、平均離反率が74%から23%へと大幅に低下することがわかる。このようにしてすべての変数について同様の検証を行うことで、ブラックボックスではわからなかった平均離反率が相対的に高いセグメントを探索的に見つけ出し※5、また意味も解釈できるようになる。
では、この残高800ポイント以下(平均離反率74%)と残高801ポイント以上(同23%)の2セグメントについて、会員ポイント残高以外の31変数がどれだけ寄与しているのだろうか?まずはこの2セグメントについて全変数の単純な平均値を比較してみよう(表2)※6。
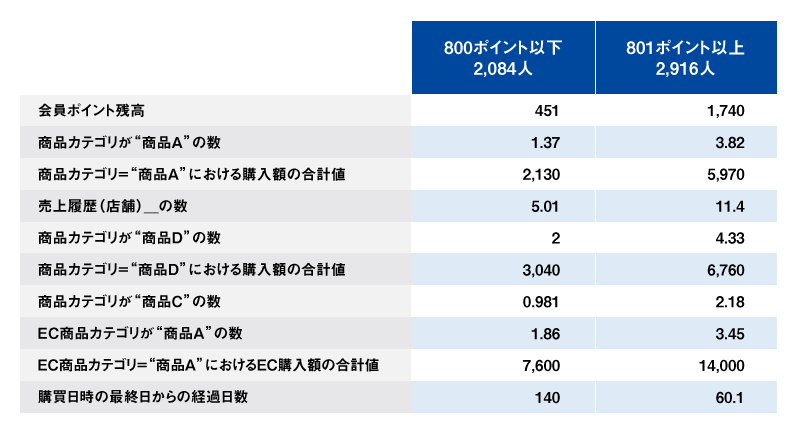
表2 2つのセグメント間での各変数の平均値の比較
その結果から2セグメント間で平均値の差が大きい変数についていくつかの値を代入してみて効果の大きさを推定し、平均離反率74%と23%の差分51Pに占める寄与の度合いをウオーターフォール型の図で表現したのが図3である※7。
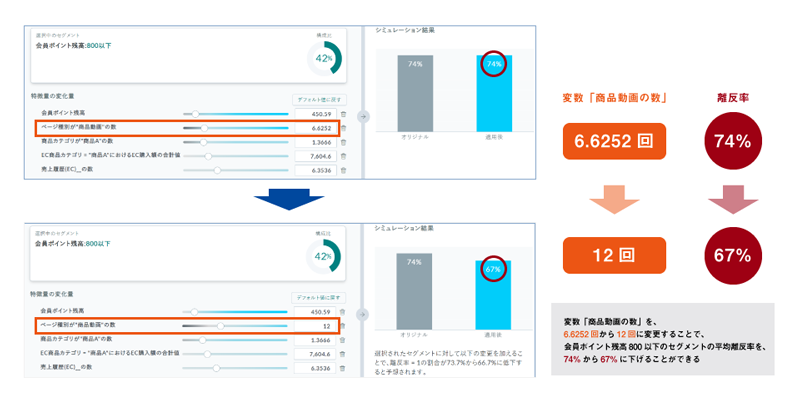
図3を見ると、この2つのセグメントの平均離反率の差分51Pのうち、2つのセグメントを作る際に使った会員ポイント残高は約24Pに相当し、次に貢献度が大きいのは「商品カテゴリAの数」でその効果は約16Pであることがわかる。ここまでわかると、次は「商品カテゴリAの数」をどのように変化させればよいのかを検証したくなるだろう。KIでは、シミュレーション機能が実装されており、図4のようにツールバーを左右させることで、平均離反率がどれだけ低下するのかを動的に参照しながらターゲットを探索することが可能になる。まさにこの作業は冒頭に述べた図1のレバーを操作して予測値の変化を見ながらチューニングするイメージに近い※8。
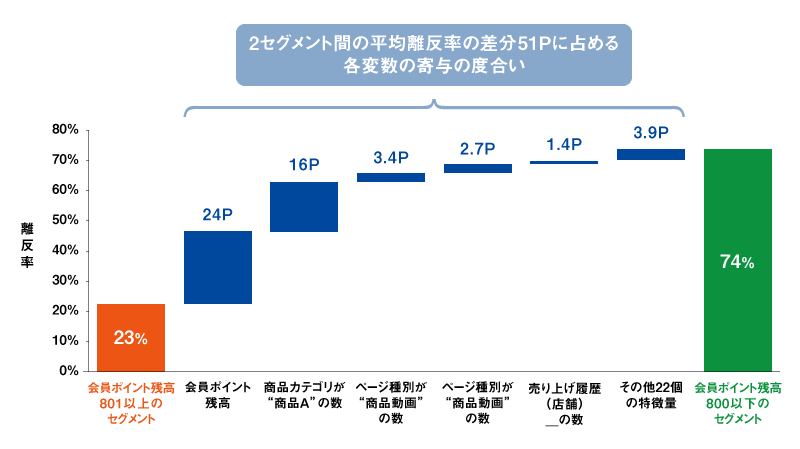
図3 どの変数が2セグメント間の平均離反率の差に寄与しているか?

※前のページへ戻るには、ウィンドウの画像が表示されていない部分をクリックするか、閉じるボタンを押してください
図4 KIによるシミュレーション
このように、仮にブラックボックス型の予測モデルであっても、離反率を下げられる余地の大きそうなセグメントの意味を理解しながら探し出し、実際にレバーを動かすようにしてしきい値を変化させながら微調整をしていくことで、「どういうセグメントを対象として切り出したのか」「その対象を選び出したのは、〇〇%の効果が見込めるからだ」など、施策の対象に解釈や理由付けを行うことができるようになる。精度の高い機械学習手法に解釈性を加えてマーケティング施策に活用できることは、マーケターにとって大きな武器になるだろう。
※1:XGBoostは機械学習アルゴリズムの1つで、勾配ブースティングと呼ばれるアンサンブル学習と決定木を組み合わせた手法であり、非常に高い識別能力と汎化能力(=未知のデータへの判別性能)を持つ。判別問題、回帰問題双方に使えるため、現在の機械学習系予測モデルの主流となっている。
※2:変数の重要度(Importance)という目安になる指標を出力することはできる。
※3:今回の事例では、キーエンス社のデータアナリティクスプラットフォーム「KI」を使用した。キーエンス社からはKIの画面イメージの提供を受けたが一部改変している。また一部の解析アルゴリズムも説明上KIとは異なるところがある。解析に使用したデータは架空のものであり、説明変数は33個、件数は5,000件、離反率は全体で44%である。予測モデルのアルゴリズムは勾配ブースティングの手法を使用した。
※4:注目している1つの変数について、それが連続変数であれば一定の範囲に区切りそれぞれの範囲での予測値の平均値を、カテゴリカル変数であればすべてのカテゴリ値についての予測値の平均値を算出する。
※5:KIでは、モデル構築後に、効果が大きい(今回の事例では平均離反率の低下の余地が大きい)セグメントを自動的に見つけ出し、その効果の大きさで一覧表示する機能が実装されている。変数を寄与の大きさ順に表示するのではなく、改善余地の大きい「セグメント」順に表示するアイディアは斬新であり、マーケターにとっては大変使いやすい。
※6:表2には32変数のうち2セグメント間で差が大きい上位10個(1つは今注目している「会員ポイント残高」)のみ表示している。
※7:図3のウオーターフォールは離反率差分の51Pを、寄与の大きい上位5変数(とその他変数の合算)の寄与の大きさで案分したもので、あくまでも目安である。
※8:図1のブラックボックス型の多数のレバーは意味が解釈できない特徴量を表しているが、KIでのシミュレーションのレバーは、ホワイトボックス型のように変数の意味が分かっているレバーを操作するイメージである点が異なることに注意したい。
渋谷直正著 連載『集まるデータ』のマーケティング活用術
著者の紹介
渋谷 直正
株式会社デジタルガレージ 執行役員 CDO(チーフデータオフィサー)
2002年に日本航空株式会社に入社。JALホームページのログ解析や顧客情報分析、航空券などのレコメンド施策の立案・企画・実施を担当。2014年、日経情報ストラテジー誌による「データサイエンティスト・オブ・ザ・イヤー」受賞。2019年より現職、デジタルガレージグループでのデータ活用を統括・推進する。ビジネスアナリティクスや実務に役立つ分析手法に詳しく、データを使ったマーケティングを得意とする。総務省統計局講座や大学での講演・記事掲載など多数。
著者の人気記事
カテゴリーから探す
タグから探す
アクセスランキング
コラムランキング
メールマガジン
マーケティングに関するホットな話題やセミナーなどの最新情報をお届けします
