集計の基本(5)
集計表を可視化する(グラフの作成)
集計表の可視化(グラフ化)の効果
アンケート調査で収集したデータの可視化には「グラフ」を用います。グラフ化は一目でデータの傾向をつかむのに有効な手段です。また、調査結果データを用いて、他者にプレゼンを行ったり、説明を行ったりする際にも、グラフで視覚的に表現することで直観的な理解を促し、説得力を高める効果があります。
一方で、データをグラフで表す際には、設問の種類に応じて適切なグラフを選ぶ必要があります。グラフの選び方を間違えると、データの読み解き方を誤ってしまうことにもつながり注意が必要です。
では、それぞれの設問には、どのグラフの種類が適しているのでしょうか。
グラフの種類と、最適な設問タイプ
円グラフ
| 最適な設問タイプ | SA(シングルアンサー、単一回答)設問 ※MA(マルチアンサー、複数回答)設問には使用できない |
|---|---|
| 特徴 | 回答全体の中での構成比(内訳)を知りたい時に最適 |
| 最適な設問タイプ | SA(シングルアンサー、単一回答)設問 ※MA(マルチアンサー、複数回答)設問には使用できない |
|---|---|
| 特長 | 回答全体の中での構成比(内訳)を知りたい時に最適 |
円グラフとは、円全体を100%として、各項目の構成比を扇形の面積で表したものです。
図1のように、SA設問の単純集計結果を可視化するのに用います。
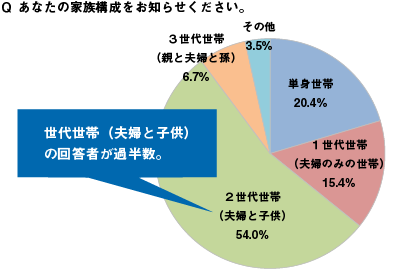
図1 円グラフ(単純集計結果の可視化)
帯グラフ(横帯グラフ)
| 最適な設問タイプ | SA(シングルアンサー、単一回答)設問 ※MA(マルチアンサー、複数回答)設問には使用できない |
|---|---|
| 特徴 | 回答全体の中での構成比(内訳)を知りたい時に最適 複数データの比較に向いている |
| 最適な設問タイプ | SA(シングルアンサー、単一回答)設問 ※MA(マルチアンサー、複数回答)設問には使用できない |
|---|---|
| 特長 | 回答全体の中での構成比(内訳)を知りたい時に最適 複数データの比較に向いている |
帯グラフとは、帯全体を100%として、各項目の構成比を長方形の面積で表したグラフです。円グラフ同様、構成比(内訳)を知りたいときに便利です。SA設問に用いられる点は円グラフと同じですが、複数の帯グラフを並べた際に比率の変化を確認しやすいため複数のデータの比較に向いています。そのため、SA設問のクロス集計結果を可視化する際によく用いられます。
図2のように、分析軸毎(図2では性別毎)の数値を比較したい際は、帯グラフを用いると違いが分かりやすくなります。

図2 横帯グラフ(性別クロス集計結果の可視化)
棒グラフ
| 最適な設問タイプ | MA(マルチアンサー、複数回答)設問 |
|---|---|
| 特徴 | 選択肢毎の回答者数(%)の大小比較に適する 値の高い項目や、低い項目を確認するのに便利 |
| 最適な設問タイプ | MA(マルチアンサー、複数回答)設問 |
|---|---|
| 特長 | 選択肢毎の回答者数(%)の大小比較に適する 値の高い項目や、低い項目を確認するのに便利 |
棒グラフとは、選択肢毎に、回答者数(%)を棒の長さで表したグラフです。
選択肢をグラフの左側に表示し棒を横向きに並べた横棒グラフ、選択肢をグラフの下側に表示し棒を縦向きに並べた「縦棒グラフ」があります。
MA設問の単純集計結果を可視化する際に用いられることが多いですが、図3のようにスコアの高い順(低い順)に選択肢を並べ替えて表示させるとより直観的に理解しやすくなります。
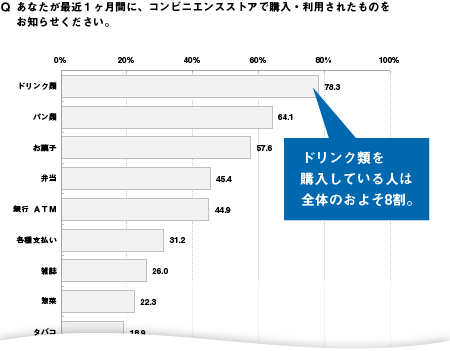
図3 横棒グラフ(MA設問の単純集計結果を可視化/値降順で並べ替え)
また、単純集計結果だけではなく、クロス集計結果も合わせて数値を確認したい場合には、図4のように縦棒グラフに数表を付加することをお勧めします。図4では、「最近1カ月以内にコンビニエンスストアで購入したもの」の単純集計結果(全体の数値)を縦棒グラフで表現し、その下に、分析軸(性別×年代別)毎の値を数表でつけたしたものです。さらに、数表部分はハッチング(網掛け)をかけて、全体との差が出ている項目をわかりやすく色づけしています。
このようなグラフ(数表)を用いると、「【全体で最も購入されているものはドリンク類】であるが、特に【男性20~40代の購入比率が高く、女性40代以降の購入比率が低い】」こと、「【全体で2番目に購入されているものはパン類】であり、【どの性年代も同じように購入している(女性30代の購入比率がやや高い)】」ことなどを読み取ることができます。
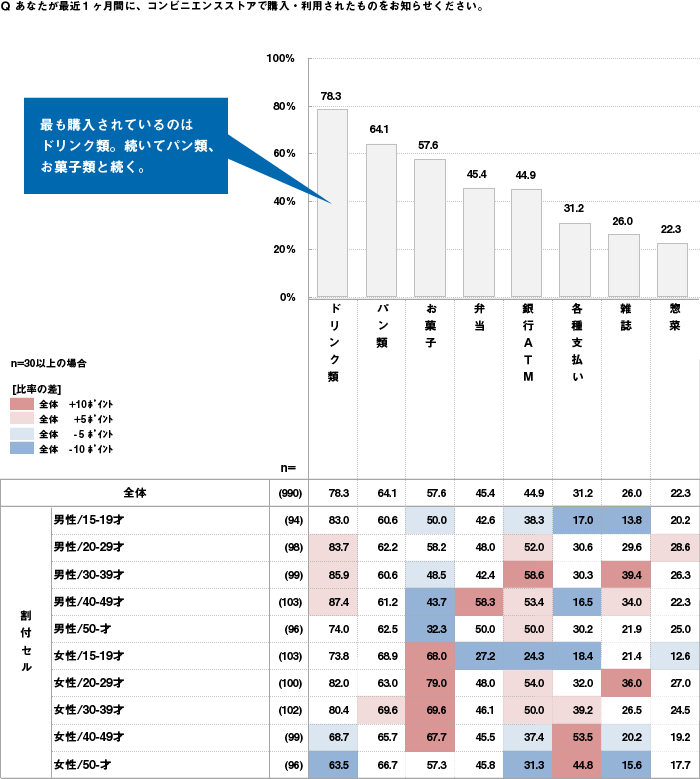
図4 縦棒グラフ+数表(MA設問の単純集計結果を可視化/クロス集計結果を付加)
折れ線グラフ
| 最適な設問タイプ | MA(マルチアンサー、複数回答)設問 |
|---|---|
| 特徴 | 連続的変化(時系列変化等)を捉えるのに適する |
| 最適な設問タイプ | MA(マルチアンサー、複数回答)設問 |
|---|---|
| 特長 | 連続的変化(時系列変化等)を捉えるのに適する |
折れ線グラフとは、横軸に項目(選択肢や時間経過)、縦軸に各項目の値をとって、線で結んだグラフを指します。線の傾きにより、値の増減が分かりやすく可視化されます。全体を通して折れ線が上昇しているか、下降しているかで値の増加(減少)の傾向をつかむことが可能となり、さらに、グラフの傾きの大きさでその変化の大きさを直観的に理解することができます。
図5のように、主に、時系列変化を可視化したい際に用いられるグラフです。このグラフを見ると、全体的に右肩上がりの傾斜になっていることが一目瞭然です。過去よりも「何か社会のための役立ちたいと思っている」人の割合が増えている傾向にあることが分かります。
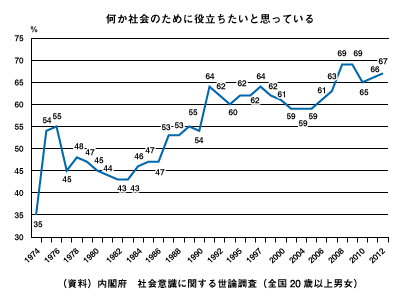
図5 折れ線グラフ(時系列変化を可視化)
棒グラフ+折れ線グラフ
| 最適な設問タイプ | MA(マルチアンサー、複数回答)設問 |
|---|---|
| 特徴 | 複数データの比較に向いている |
| 最適な設問タイプ | MA(マルチアンサー、複数回答)設問 |
|---|---|
| 特徴 | 複数データの比較に向いている |
棒グラフは選択肢毎の回答者の大小の比較に向いていると述べました。複数の分析軸での比較にはあまり向きません。分析軸を加えたクロス集計結果も含めて、視覚的・直観的にすばやく理解させたい時には、棒グラフと折れ線グラフを組み合わせて表現することがお勧めです。棒グラフで単純集計結果をあらわし、分析軸毎の比較対象を折れ線グラフで表すことが一般的です。
図4の場合を見てみましょう。数表を読み込むことで、性別×年代別の傾向を読み解くことは可能ですが、直観的に男性の傾向・女性の傾向をつかむことは困難です。そこで、男性の値、女性の値をそれぞれ折れ線グラフにして、全体値をあらわす棒グラフに重ねて表現します(図6)。そうすることによって、棒グラフのみではわかりにくかった性別の傾向を可視化させ、直観的に理解しやすくなります。
なお、図6では「性別(男性・女性)」のデータのみを折れ線グラフで表現しました。「割付セル(男性/15~19才・・)」も折れ線グラフに含んでしまうと折れ線の数が多くなりすぎ、グラフが見づらくなってしまいます。そのため特に結果に注目したい項目のみに絞り、折れ線の数は多くとも5~6本程度までに表示させるようにします。
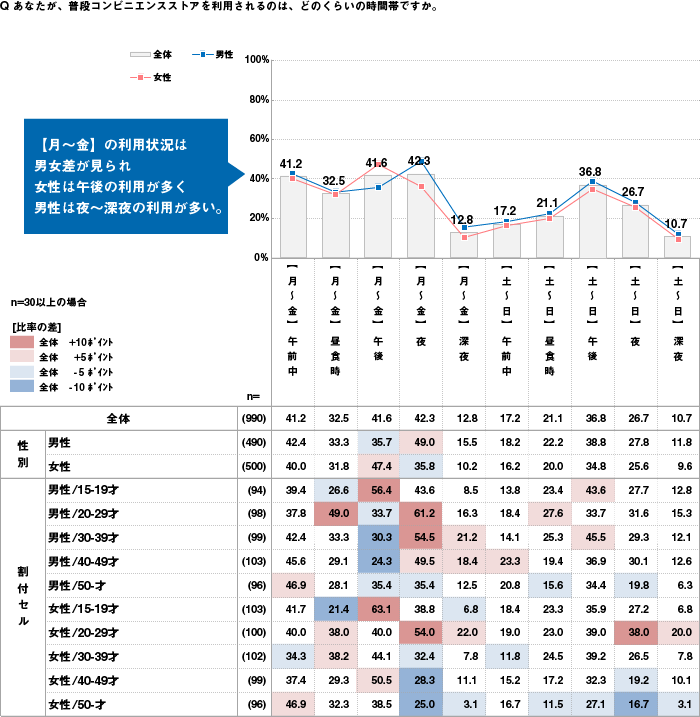
図6 棒グラフ+折れ線グラフ+数表(MA設問の単純集計結果+クロス集計結果(比較対象)を可視化)
- お問い合わせ・集計ソフトのダウンロードはこちら
Myリサーチページログイン








